Algorim Lecture 2-Amortized Analysis
Amortized Analysis: Adding Things in Smart ways.
Lots of analyses get easier when you add things together after re-grouping them in smart ways.
Introduce
Example: Think about an Algorithm from the Perspective of a Data Element…
Example: Merge Sort
It takes Θ(n) time to merge two sorted lists of conbined length n.

Think about the runtime level by level. Each level, the runtime is O(n). Each element have one time to merge.
If I am is one element, one element runtime is the O(logn).
How much of work in the function for one element.
Figure out
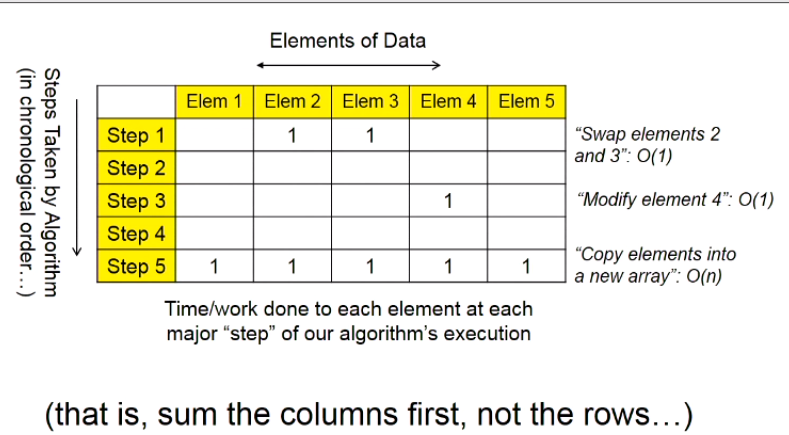
how much work / running times is spent on a single generic element of dataduring the course of the algorithm.Add this up to get the total running time. (Compared to adding up the time spent on each “operation”, summed over each operation in chronological order)
Example: Enumerating Subsets
counter = 0
For all subsets S ⊆ {1, 2, 3, 4 ... n},
increment counter.
What is the value of counter at the end of execution?
Counter = n*n
Just two steps for each element, in the subset or not in the subset.
Think about the next one:
For all subsets S ⊆ {1, 2, 3, 4 ... n},
For all subsets T ⊆ S
Increment Counter
Now, what is the value of counter at the end of execution?
If you thinking about the each subset, this is a confused way because some subsets are big and others are small. By this question, we can thing about the element by data.
So, each element can be in three ways: In S but not T, In S and T, not in S and T.
Counter: n * n * n
Example: Domination Radius
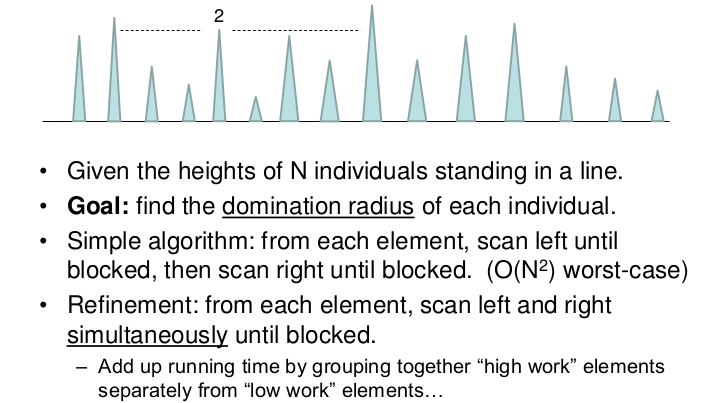
- Given the heights of N individuals standing in a line.
- Goal: Find the domination radius of each individual.
In this problem, each one will expand both left and right sides. Then, this solution need n expand time in the code. However, we want the solve this question in O(nlog n)
Solution 1: Simple algorithm: from each element, scan left until blocked, then scan right until blocked.
Running times: O($n^2$) worst-case
There is an issue with this solution, if the element have been sorted and you go to the wrong way firstly, then you will get into trouble.
Solution 2: Refinement- From each element, scan left and right simultaneously until blocked.
Running times: O($n^2$) worst-case
For each element in this array, they may have different worst time. The tallest one have the different worst time with the shortest one. The very tall people may spend a lot of works. and the lower one may only spend a few works. So, how we can get the worst-time for this solution, different element have the different worst-time in this case. Their behaivir is totoally different.
High-Work: Scan $\geq$ D, So, total: O($ \frac{n}{D}*n $ )
Low-Work: Scan $\leq$ D (the work per element), So,total: O(n*D)
n is the # of the number of element in the array, so the worst work for each element is n. And How many elements for the high works: n/D because if the D is the each high-work element’s interval. If the interval is less than D, then the scan > D is error. THe number of high element is n/D
From the above, the total running times: O($\frac{n^2}{D} + nD$), in this case, if we choose the D is with small, the first value will be very big. However, if we choose the D is very big, the second value will be very big even though the first value change to the small value. What is the best way we can get the best running times?
When the $D = \sqrt{n}$, we can get the best running times: O($n^{1.5} + n^{1.5}$) = O($2*n^{1.5}$)
In this case, if we have a sorted array:
The running times is:
$1 + 2 + 3 + … + n = \frac{n(n+1)}{2} = \Theta(n^2)$
Now, let’s us to thing about how to build these element more than three groups.
| Work/Element | Range | Max Number of Element | Total |
|---|---|---|---|
| First Group | [n/2, n) | 2 of them | O(n) |
| Second Group | [n/4, n/2) | 4 of them | O(n) |
| Third Group | [n/8, n/4) | 8 of them | O(n) |
| … | … | … | … |
So, in this case, we get the total times: O(nlog n)
Re-Sizing Memory Blocks
There are some questions for the Re-Sizing Memory Blocks:
- Since Memory blocks often cannot expand after allocation, what do we do when a memory block fills up?
- For example, suppose we allocate 100 words of memory space for a stack (implemented as an array), but then realize we have more than 100 elements to push onto the stack!
Of course, if we use a linked list would have solved this problem, but suppose we really want to use arrays instead…)
Some exixt solution for this problem
- A common technique for block expansion: Whenever our current block fills up, allocate a new block of twice its size and transfer the contents to the new block.
- Unforturnaely, now some of our push operations will be quite slow!
- Most push operations take only O(1) time.
- However, a push operation resulting in an expansion (and a copy of the n elements currently in the stack) will take $\Theta$(n) times.
So, what is the runtimes for the push.(It is hard to say.)
Push has a somewhat not-uniform running time profile:
- O(1) almost always
- Except $\Theta$(N) every now and then.
But just saying the running time is “$\Theta$(N) in the worst case” doesn’t tell the whole story..
- Doesn’t do the structure justive.
- People might be scared to use it for large input sizes…
Most times, it is so fast. So, for these case, we need a new way to descript this case, it’s bad to misunderstanding for the only past descript.
How much does each push actually cost?
If we insert the element in the stack(array)
And, what about if we charge ourselves 3 units of work per operation instead…?
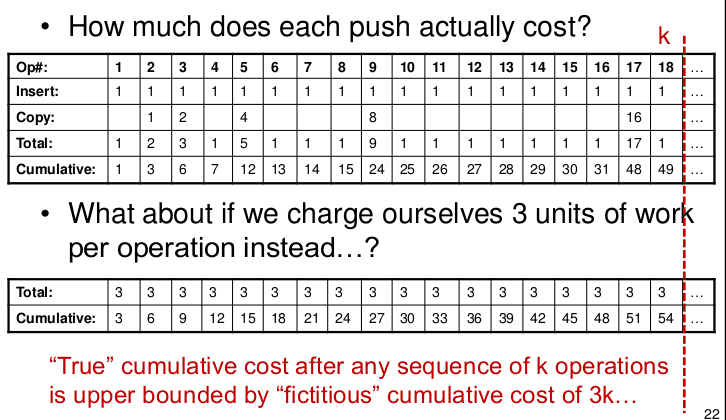
True cumulative cost after any sequence of k operations is upper bounded by fictitious cumulative cost of 3k…
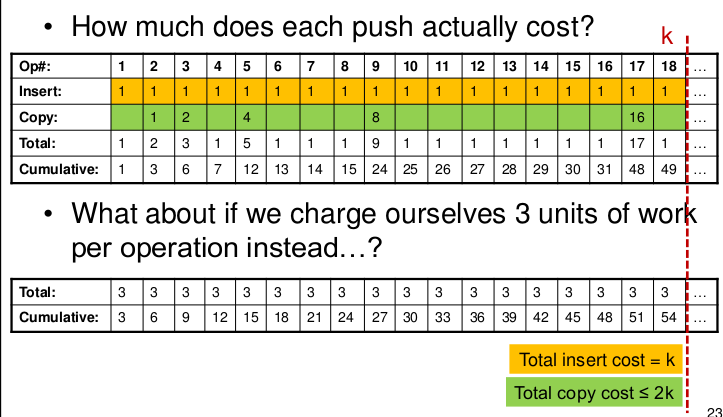
And, if we change something:
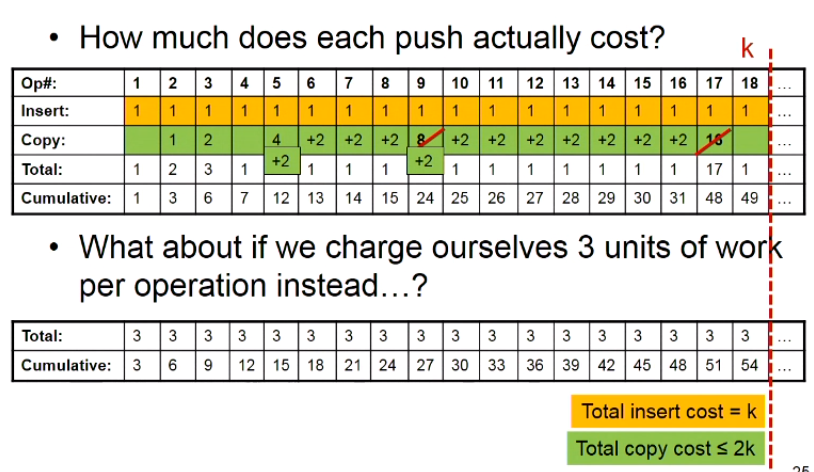
So, how different is our version of push from a version that takes 3 units in the worst case?
Amortized Analysis
Any sequence of k pushes takes O(k) worst-case time, so we say that push takes O(1) amortized time.
On average, over the entire sequence, each individual push therefore takes O(1) time.
In general, an operation runs in O(f(n)) amortized time if any sequence of k such operations runs in O(k * f(n)) time.
The motivation for the Amortized Analysis
Amortized analysis is an ideal way to characterize the worst-case running time of operations with highly non-uniform performance.
It is still worst-case analysis, just averaged over an arbitrary sequence of operations. And, it gives us a much clearer picture of the true performance of a data structure that more faithfully describes the true performance. (For example, $\Theta(N)$ worst case vs. O(1) amortized.)
Example
Suppose we have 2 implementations of a data structure to choose from:
- O(log n) worst-case time / operation
- O(log n) amortized time / operation
There is no difference if we use either A or B as part of a larger algorithm. For example, if our algorithm makes n calls to the data structure, the running time is O(n log n) in either case.
The choice between A and B only matters in a “real-time” setting when the response time of an individual operation is important.
If the dataset is not big, you want to as fast as they can. Then choose the first one.
Generalizing to Multiple operations
We say an operation A requires O(f(n)) amortized time if any sequence of k invocations of A requires O(k f(n)) time in the worst case.
We say operations A and B have amortized running times of O($f_A(n)$) and O($f_B(n)$) if any sequence containing $K_A$ invocations of A and $K_B$ invocations of B requires: $O(K_A f_A(n) + K_B f_B(n))$. And so on, for 3 or more operations…
A simple, but often limited, method for Amortized analysis
Compute the worst-case running time for an arbitrary sequence of k operations, then divide by k. Unfortunately, it is often hard to bound the running time of an arbitrary sequence of k operations.(Especially if the operations are of several types – for example, “push” and “pop”)…
Accounting Method Analysis
Example Using Memory Re-Sizing
Charge 3 units (i.e., O(1) amortized time) for each push operation.
- 1 unit for the immediate push.
- “$2” credit for future memory expansions.

You charged upfront and use it later. Ans the dataset is not changed. Just make this quesiton like you pay for the car fees which we talked before.
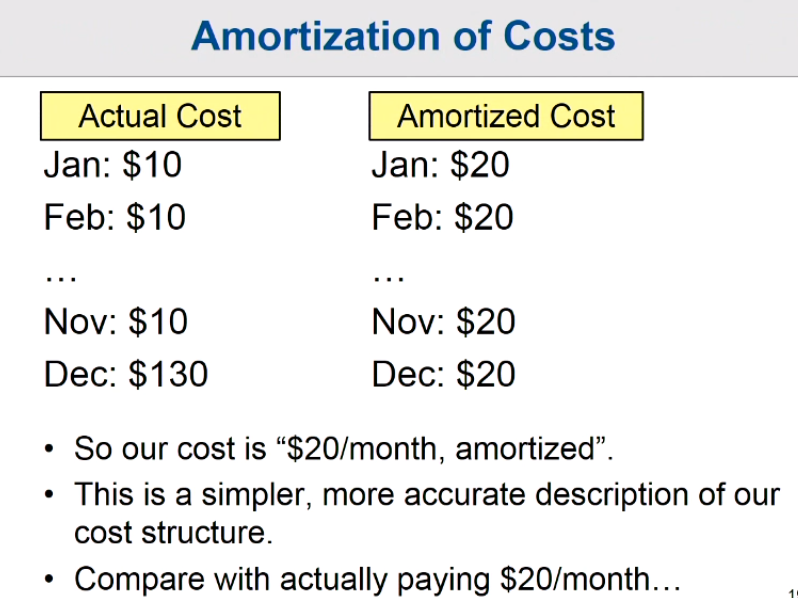
There are the same thing, pay for the cost which you may be used in the future. The data you need pay for is not changed, just make each step siilar.
What about adding “Pop” - Will this work well?
When the buffer fills up due to too many pushes, double its size. And when the buffer becomes less than half full due to too many pops, halve its size. We want think about how to make the most space in the buffer are effective.
If we use the half of the buffer as the line to detect double its size or half its size, this buffer may double and half frequently if these data size close with the half of buffer size.
Change to When the buffer becomes less than one quarter full due to too many pops, halve its size. When the buffer fills up due to too many pushes, double its size.
Example: The Min-Queue
Using either a linked list or a (circular) array, it is easy to implement a FIFO queue supporting the insert and delete operations both in O(1) worst-case time.
Suppose that we also want to support a find-min-operation, which returns the value of the minimum element currently present in the queue.It is possible to implement a “min-queue” supporting insert, delete, and find-min all in O(1) worst-case time?
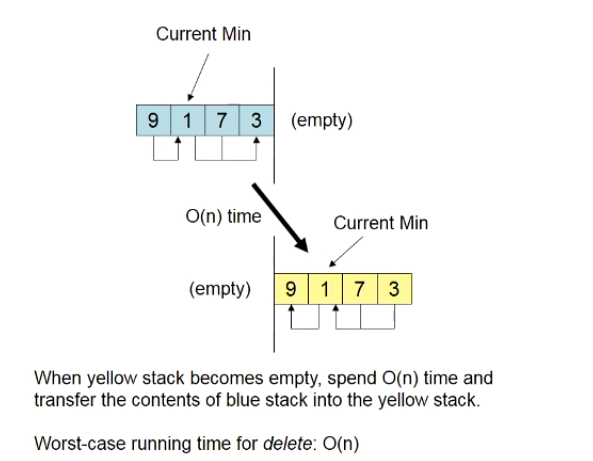
If we use a new structure about the Min-Queue as a Pair of “Back-to-Back” Min-Stacks.
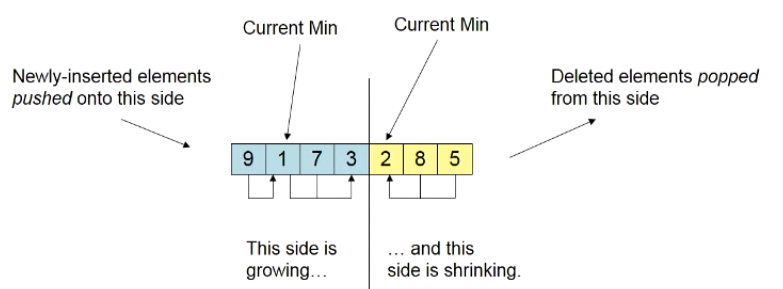
We insert the data at the blue side, and delete the element at the yellow side. And, what will waste a lot of time in this case?
When yellow stack becomes empty, spend O(n) time and transfer the contents of blue stack into the yellow stacks. Just like the blue stack pop and the yellow stack push the element in the stack.